Route Optimization: Your Complete Guide to Efficient Deliveries

Introduction

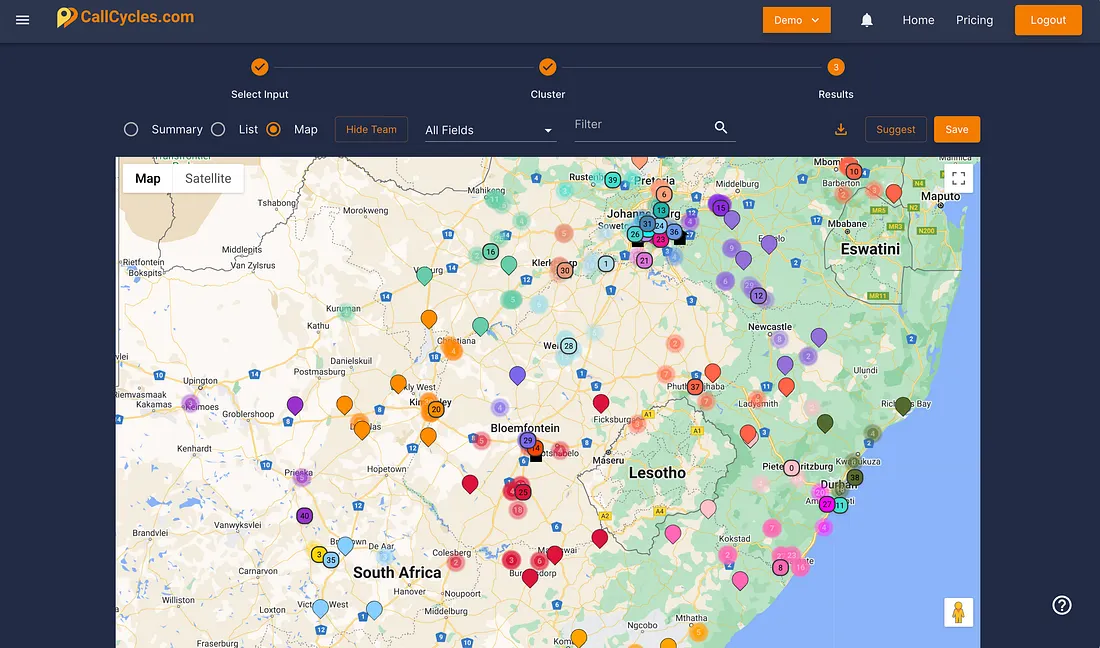
What happens in most companies, is you start of with a GREAT spread of customers over your sales force. Then, over time, the waters get muddied and a few years down the line you probably have something similar to figure

1. Note the different colors, denotes different rep's and see how much they overlap. This article will deal with sorting this mess out.

For a stress-free solution, check out callcycles.com. Say goodbye to coding as we've got you covered, and then some.

If you have not worked with KMEAN's, then here is a good article.

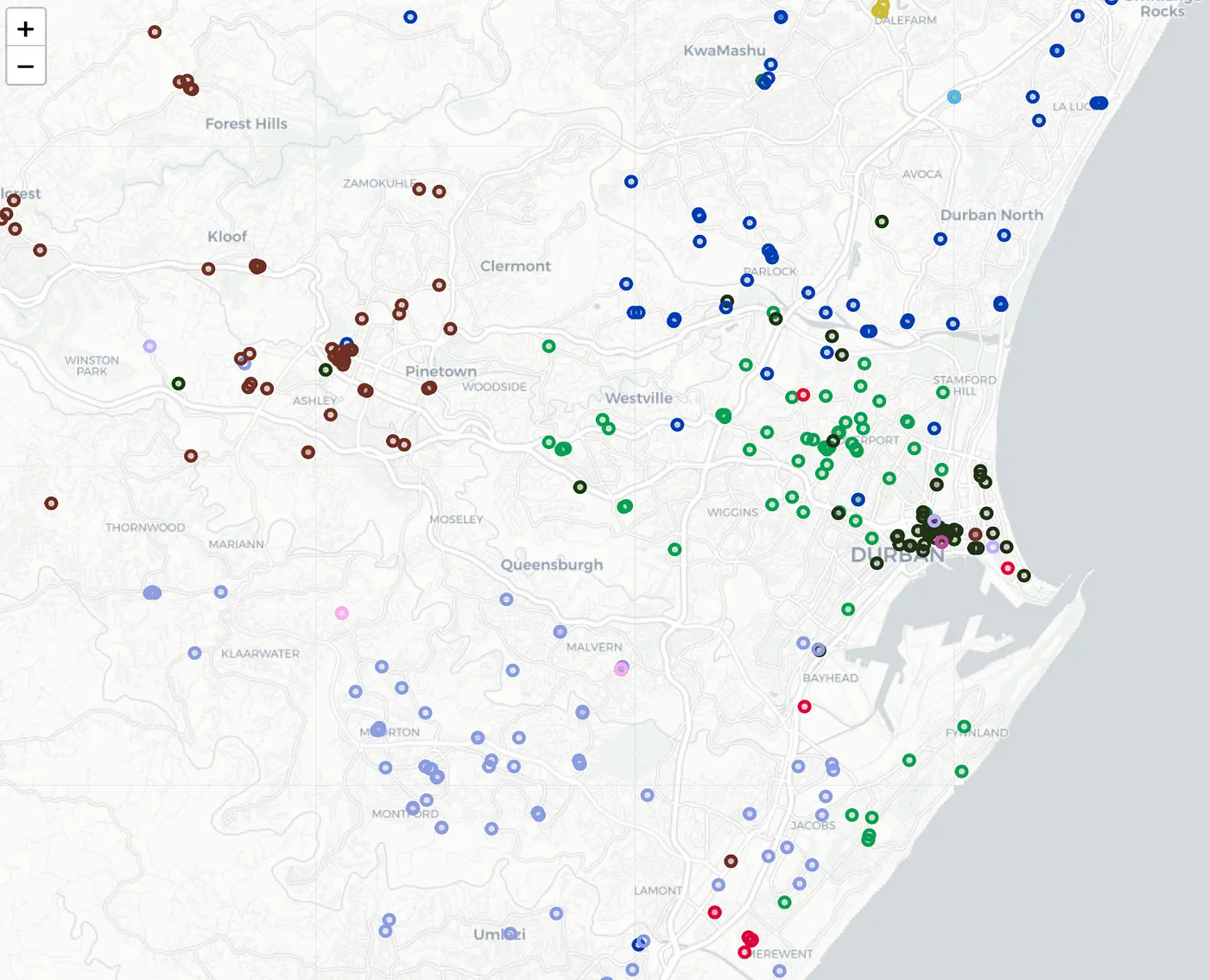
Figure 1: sales force geographically spread

Required packages

We will be using KMEAN's as our initial algorithm to group the customers according to their locations. However, usual KMEAN's doesn't quite do the trick in our scenario, since KMEAN's can end up with very unbalanced area's. One rep could end up with 20 customers and another could end up with 150. So k-means-constrained to the rescue. We can give minimum and maximum for each area. So, first up, install using pip.

pip install k-means-constrained

Now, lets import the packages we need

            import numpy as np
            import pandas as pd
            import matplotlib.pyplot as plt
            import folium
            from k_means_constrained import KMeansConstrained
          

Importing your data

Now import your data into a data frame as I have below in figure 2. I have blocked out some data, but you get the point, you need the following fields:

AccountID — the customers account numer
RepID — The sales representative linked to the customer
Latitude
Longitude
Location — A simple concat of latitude,longitude

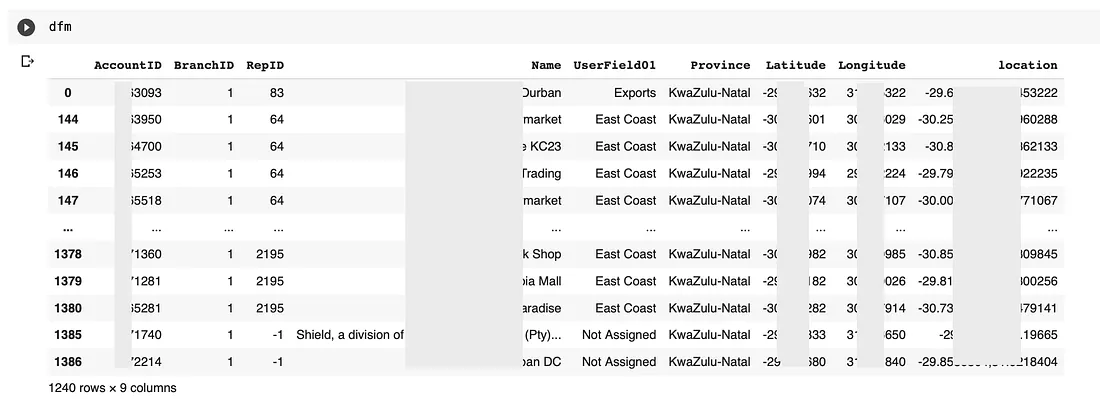
Figure 2: Dataframe once its populated

Plotting the initial data

You can use below to plot the existing customer base with each representative as a different colour.

            lst_reps = sorted(list(dfm.RepID.unique()))
            k = len(lst_reps) - 1
            # Get our list of unique clusters
            lst_elements = sorted(list(dfm.RepID.unique()))
            # Now make up random colors for each unique RepID
            lst_colors = ['#%06X' % np.random.randint(0, 0xFFFFFF) for i in
              range(len(lst_elements))]
            # Add color column to dataframe and apply colors
            dfm["color"] = dfm["RepID"]
            dfm["color"] = dfm["color"].apply(lambda x:
              lst_colors[lst_elements.index(x)])
            m = folium.Map(tiles="cartodbpositron", zoom_start=11)
            for index, row in dfm2.iterrows():
             folium.CircleMarker(
            
              location=[float(row['Latitude']), float(row['Longitude'])],
             radius=4,
            
              popup=str(row['AccountID']+'|'+str(row['RepID'])+'|'+row['Name']+'|'+row['UserField01']),
             color=row['color'],
             fill=True,
             fill_color=row['color'],
             ).add_to(m)
          

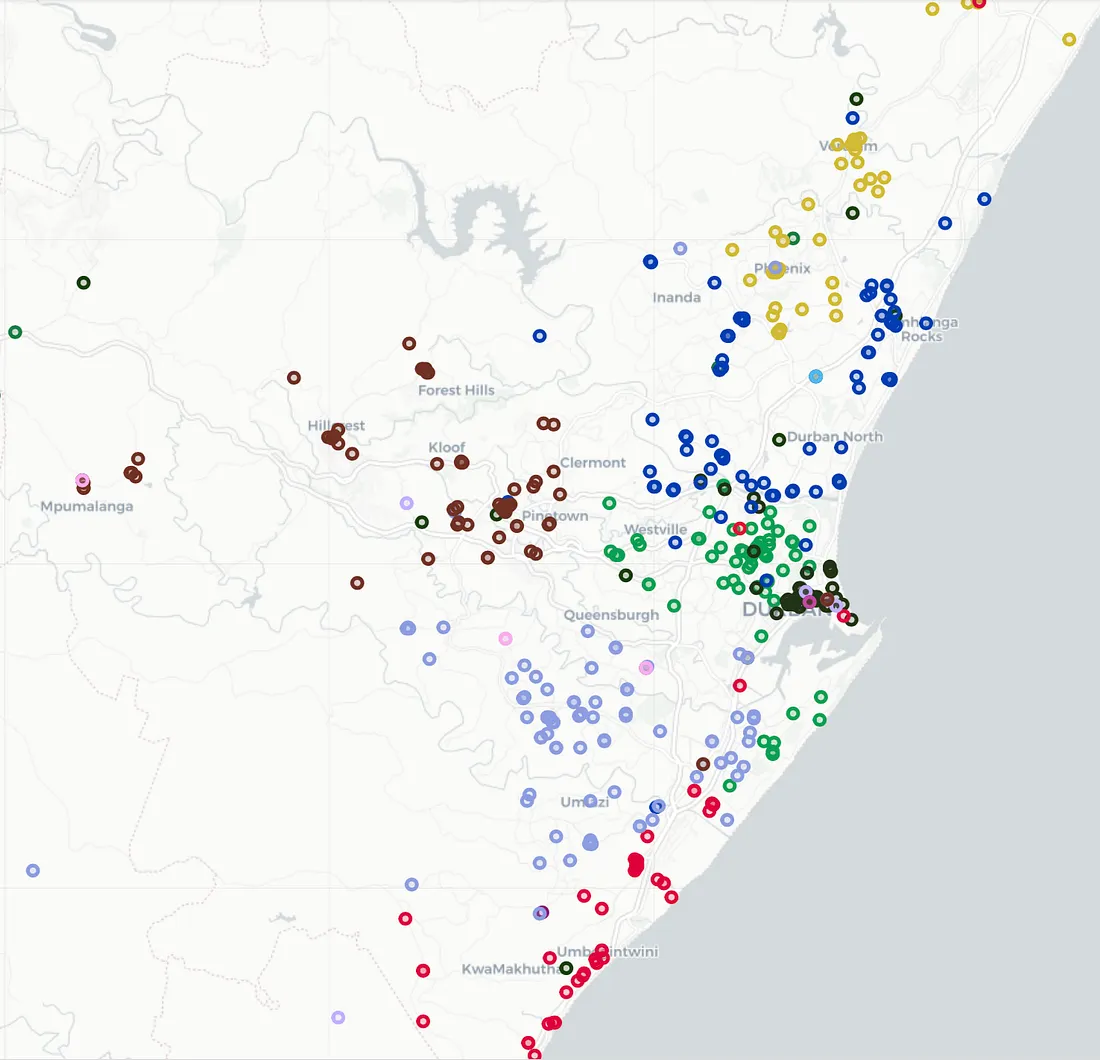
Figure 3: note the overlap of representatives

Training parameters

Let's set up out training parameters.

We want a minimum of 45 customers per representative
RepID — The sales representative linked to the customer
A maximum of 92 customers per representative

            lst_reps = sorted(list(dfm.RepID.unique()))
            k = len(lst_reps) -2
            min_customers = 45
            import folium
            max_customers = 92
          

KMEAN's to cluster our customers

Now, lets set up our KMEAN's parameters and run fit_predict. Importantly, we will want to save the centroids for each cluster.

In our case, each centroid will be a central location for each representatives area or territory.

            ## Create a new dataframe with latitude/longitude
            X = dfm[['Latitude','Longitude']]
            df_X = X.copy()
            ### KMeansConstrained parameters
            clf = KMeansConstrained(
             n_clusters=k,
             size_min=min_customers,
             size_max=max_customers,
             random_state=0
            )
            clf.fit_predict(df_X)
            # save results
            th_centroids = clf.cluster_centers_
            df_clustercentroids = pd.DataFrame(th_centroids)
            df_clustercentroids.columns = ['Latitude','Longitude']
            print(clf.inertia_)
            # send back into dataframe and display it
            dfm['cluster1'] = clf.labels_
            dfm.head()
          

Your result is now as below, take note of the new fields in our dataframe

cluster1 — The cluster

Figure 3: Results of KMEANS

Assign each cluster to the most common representative

A little like the highest common denominator, lets use an APPLY to find the most common representative in a cluster and assign them to the whole cluster.

            # get a copy of the dataframe
            dfn = dfm.copy()
            clusters = dfn.cluster1.unique()
            # Remove unwanted reps
            dfn = dfn.loc[dfn['RepID'] != 2195]
            dfn = dfn.loc[dfn['RepID'] != -1]
            # Iterate through the unique clusters
            for cluster in clusters:
            
              # find the most common rep in the cluster
            
              repid = dfn.loc[dfn.cluster1 == cluster].RepID.mode()
              #.loc[0]
             if repid.size == 1:
             repid = int(repid.loc[0])
             else:
             repid = 9999
             # assign the cluster to its repid
            
              print(str(repid) + ':' + str(cluster))
            
              dfm.loc[dfm.cluster1 == cluster,'RepID1'] = repid
            
              # Remove rep from dataframe copy so that its not used again
             dfn = dfn.loc[dfn.RepID != repid]
            dfm = dfm.astype({"RepID1": int})
          

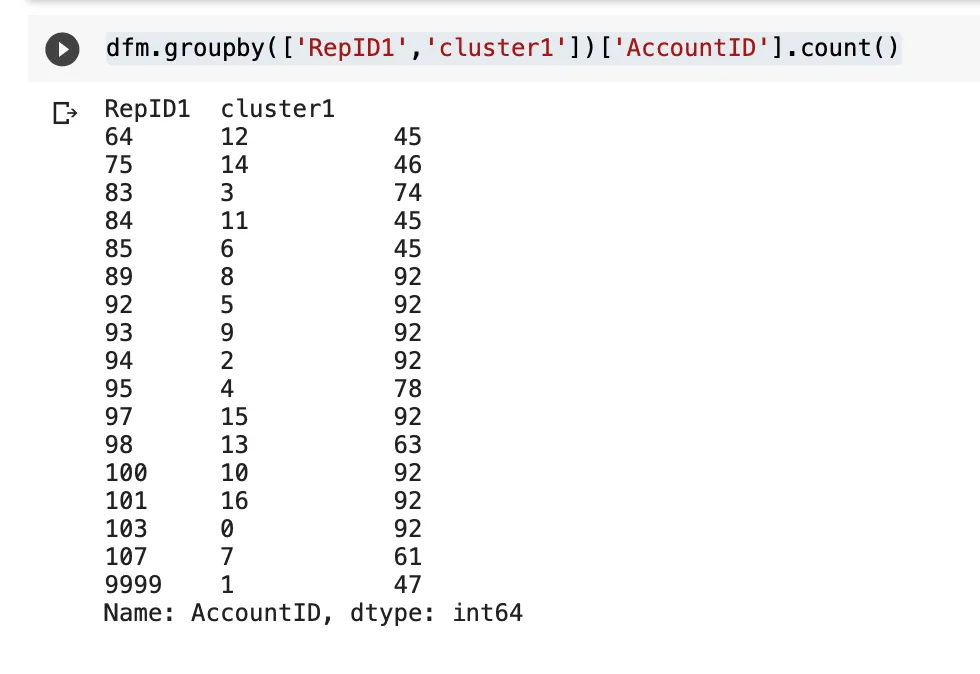
You can also see a count of how many customers have been clustered per representative:

dfm.groupby(['RepID1','cluster1'])['AccountID'].count()

Update centroids

Let's update the repID's to the centroid as well, just for info purposes

            df_clustercentroids['cluster'] = df_clustercentroids.index
            df_clustercentroids['RepID'] = df_clustercentroids.apply(lambda
              row:
            
            -1 if dfm.loc[dfm.cluster1==row.cluster].RepID1.mode().size == 0
              else
            dfm.loc[dfm.cluster1==row.cluster].RepID1.mode()[0],axis=1)
            df_clustercentroids.head(20)
          

Plot the results

Now, lets plot the results and see how we are fairing

            # Get our list of unique clusters
            lst_elements = sorted(list(dfm.cluster1.unique()))
            # Now make up random colors for each unique cluster
            lst_colors = ['#%06X' % np.random.randint(0, 0xFFFFFF) for i in
              range(len(lst_elements))]
            # Add color column to dataframe and apply colors
            dfm['color'] = dfm['cluster1']
            dfm['color'] = dfm['color'].apply(lambda x:
              lst_colors[lst_elements.index(x)])
            m = folium.Map(tiles='cartodbpositron', zoom_start=11)
            for index, row in dfm.iterrows():
             folium.CircleMarker(
            
              location=[float(row['Latitude']), float(row['Longitude'])],
             radius=4,
             popup=str(row['cluster1']),
             color=row['color'],
             fill=True,
             fill_color=row['color'],
            
              tooltip=str(row['cluster1']) + '|' + row.AccountID
             ).add_to(m)
            # Plot centroids
            for index, row in df_clustercentroids.iterrows():
             folium.Marker(
             location=row,
             popup=str(index),
            
              tooltip=str(index) + '|#=' +
              str(dfm.loc[dfm.cluster1==index].groupby(['cluster1'])['AccountID'].count().iloc[0])
             ).add_to(m)
            m
          

As you can see, we are already doing much better and plotting the centroids also gives us the central location for each area.

So, whats the problem?

Well, KMEANS-constrained is great, but the constraints now cause a few outliers which we can use KNN to resolve. Figure 5 highlights the issue for you. Can you see one customer assigned to the brown representative, BUT it doesn't make sense…. It should actually be with the purple representative.

Easy to spot on a map and lets use KNN to resolve this. If you do not know the KNN algorithm, then have a look at this article.

KNN to the rescue

First up, lets setup a train and test dataset.

            # Import train_test_split function
            from sklearn.model_selection import train_test_split
            # Split dataset into training set and test set
            X_train, X_test, y_train, y_test =
              train_test_split(dfm[['Latitude','Longitude']], dfm[['cluster1']],
              test_size=0.3) # 70% training and 30% test
          

Now that we classified our data using KMEAN's, lets train a KNN model to predict based on the KMEAN's results. This will help us with the following

1. Identify the outliers from KMEAN's due to its min/max constraints.
2. Have a model we can use going forward to predict which representative an account should be assigned to.

Now that we trained, lets run a prediction on our test set and then measure accuracy. We should see above 92% accuracy of our model

            # Import knearest neighbors Classifier model
            from sklearn.neighbors import KNeighborsClassifier
            from sklearn import metrics
            # Create KNN Classifier
            knn = KNeighborsClassifier(n_neighbors=k)
            # Train the model using the training sets
            knn.fit(X_train, y_train)
            # Predict the response for test dataset
            y_pred = knn.predict(X_test)
            # Model Accuracy, how often is the classifier correct?
            print('Accuracy:',metrics.accuracy_score(y_test, y_pred))
          

Predict on ALL data

We have a KNN model, so lets predict for latitude/longitude on our entire dataset. This will help show us some outliers where KMEAN's made an odd choice due to the constraint of min/max customers per rep.

y_pred = knn.predict(dfm[['Latitude','Longitude']])

Update the predictions to our dataframe and mark the failed knnfailer=true when KNN did not agree with KMEANS. New clusters will be in the cluster2 column.

            dfm['cluster2'] = y_pred
            dfm['outlier'] = dfm.apply(lambda row: False if row.cluster1 ==
              row.cluster2 else True, axis=1)
            dfm[dfm.cluster1 != dfm.cluster2]
          

Note the results in figure 6 with our 2 new columns. The handy outlier field tells us if KNN changed the customer to a new area.

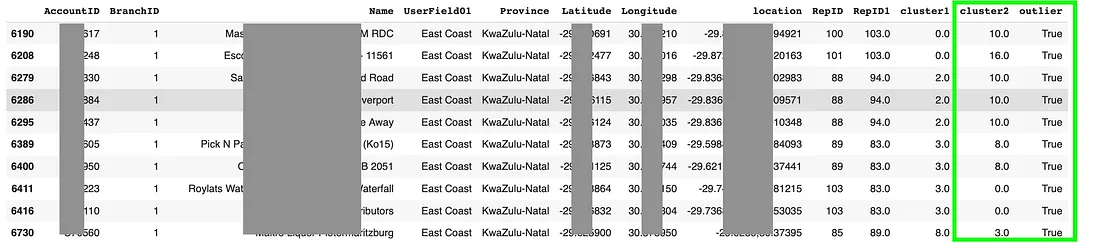
Figure 6: Results with outliers identified

Update RepID2 from most common RepID1 in cluster

In this step, lets create a repid2 in the cluster are all assigned to the most common RepID1 in the cluster 1. This ensures the outliers get the correct rep code into RepID2.

            def getMostCommonRep(row):
             global dfm
            
              repid = dfm.loc[dfm.cluster1 == row.cluster2].RepID1.mode()
             if repid.size == 1:
             return repid.loc[0]
             else:
             return -1
            dfm['RepID2'] = dfm.apply(lambda row: getMostCommonRep(row),
              axis=1)
            dfm = dfm.astype({'RepID': 'int32'})
            dfm = dfm.astype({'RepID1': 'int32'})
            dfm = dfm.astype({'RepID2': 'int32'})
            dfm = dfm.astype({'cluster1': 'int32'})
            dfm = dfm.astype({'cluster2': 'int32'})
            dfm.head(20)
          

Lets plot the new results

Now lets plot our results to see if KNN solved our outlier problem:

            # Get our list of unique clusters
            lst_elements = sorted(list(dfm.cluster2.unique()))
            # Now make up random colors for each unique cluster
            lst_colors = ['#%06X' % np.random.randint(0, 0xFFFFFF) for i in
              range(len(lst_elements))]
            # Add color column to dataframe and apply colors
            dfm['color'] = dfm['cluster2']
            dfm['color'] = dfm['color'].apply(lambda x:
              lst_colors[lst_elements.index(x)])
            m = folium.Map(tiles='cartodbpositron', zoom_start=11)
            for index, row in dfm[dfm.outlier == False].iterrows():
             folium.CircleMarker(
            
              location=[float(row['Latitude']), float(row['Longitude'])],
             radius=4,
             popup=str(row['cluster2']),
             color=row['color'],
             fill=True,
             fill_color=row['color'],
            
              tooltip=str(row['cluster2']) + '|' + str(row['RepID2']) + '|' +
              row.AccountID
             ).add_to(m)
            # Plot centroids
            for index, row in dfm[dfm.outlier == True].iterrows():
             folium.CircleMarker(
            
              location=[float(row['Latitude']), float(row['Longitude'])],
             radius=7,
             popup=str(row['cluster2']),
             color='black',
             fill=True,
             fill_color='black',
            
              tooltip='old=' + str(row['cluster1']) + '| new=' +
              str(row['cluster2']) + '|' + row.AccountID
             ).add_to(m)
            m
          

Great, as you can see in figure 7, our outlier has been reassigned to the purple representative. Note, we do give it a black border so we can easily pick the outliers out.

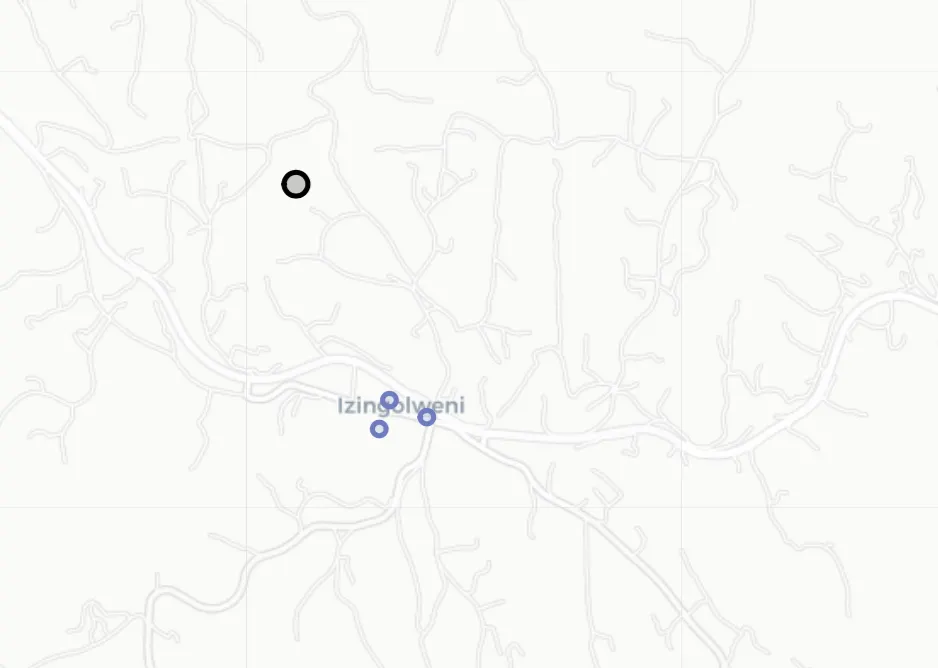
Figure 7: Final results with outliers fixed and repositioned

Boost Sales Efficiency by harnessing K-Means and KNN for Geospatial Customer Optimization